索引结构

复习提纲

1、顺序文件上的索引：密集索引和稀疏索引

2、非顺序文件上的辅助索引

3、散列表、动态散列*

4、B+ Tree*

顺序文件的索引

索引的功能：查找键 → 页号

顺序文件：记录按查找键排序（一般就是主键了）

• 密集索引
  • 每个记录都有一个索引项 ，索引项按查找键排序
  • 记录通常比索引项要大（假设）
  • 索引可以常驻内存 ==> 占用空间大
  • 要查找键值为K的记录是否存在，不需要访问 磁盘数据块
• 稀疏索引
  • 仅部分记录有索引项， 一般情况下为每个数据块的第一个记录建立 索引
  • 同样的记录可以使用更少的索引项，节省了索引空间
  • 确认是否存在键值为K的记录需要访问磁 盘数据块
• 多级索引
  • 一级索引可能还太大而不能常驻内存
  • 二级索引更小，可以常驻内存
  • 减少磁盘I/O次数
  • 维护二级索引结构代价大

非顺序文件的辅助索引

• 数据文件不需要按查找键有序（一般是主键之外的属性）
• 根据索引值不能确定记录在文件中的顺序
• 辅助索引只能是密集索引

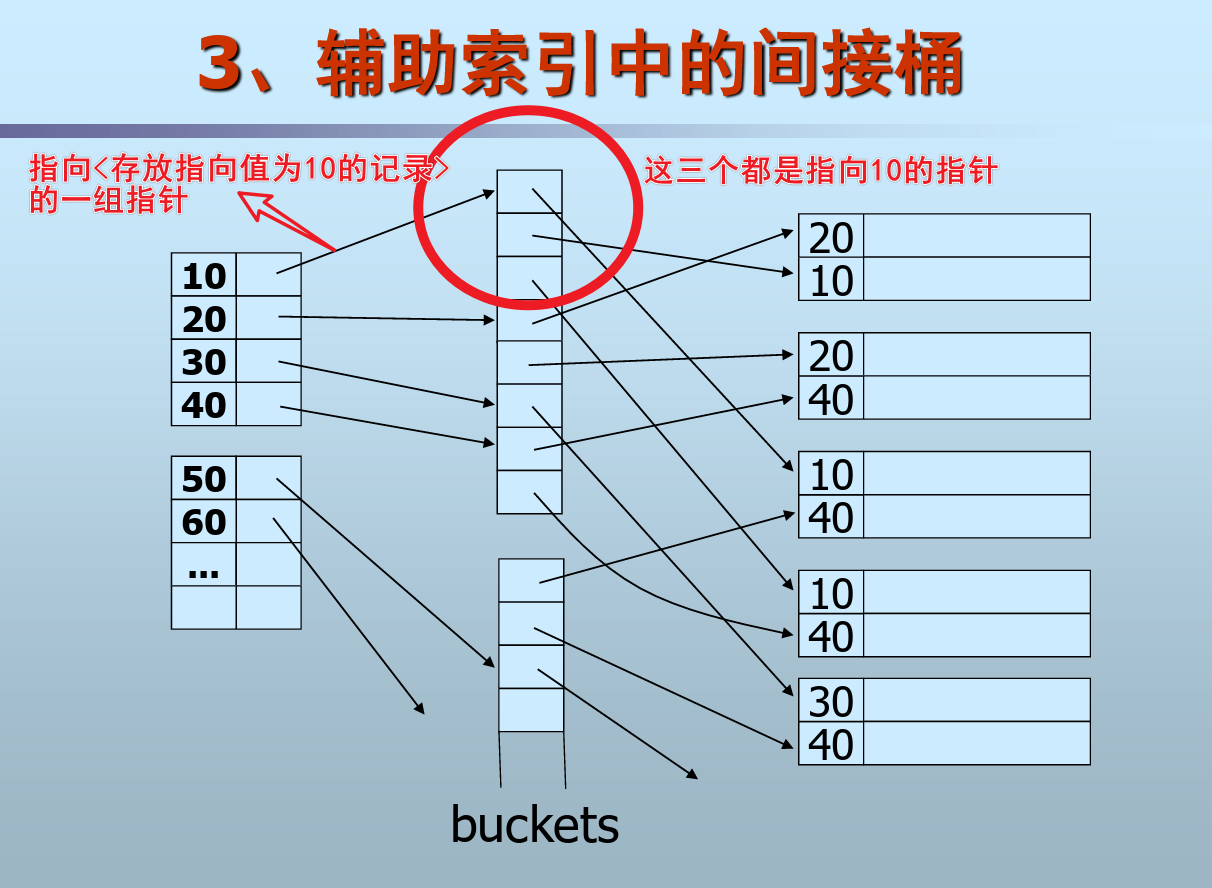
重复键值的情形——间接桶

• 仍然采用密集索引的方法浪费空间，引入间接桶机制
• 间接桶就是在辅助索引和数据文件之间的一种类似二级索引的指针表

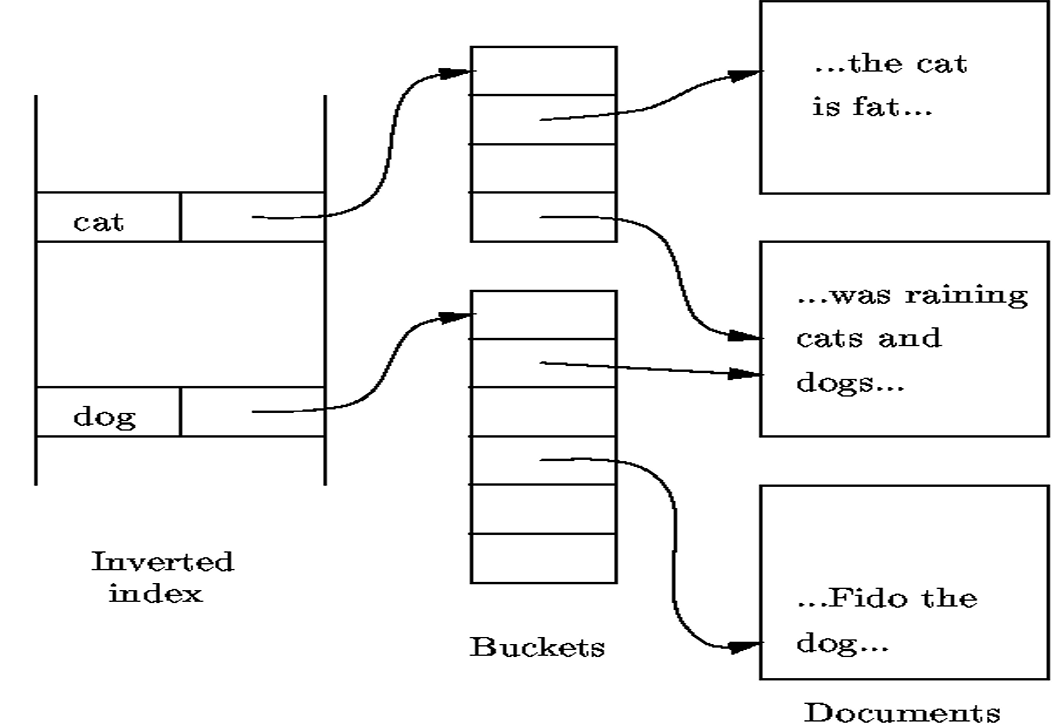
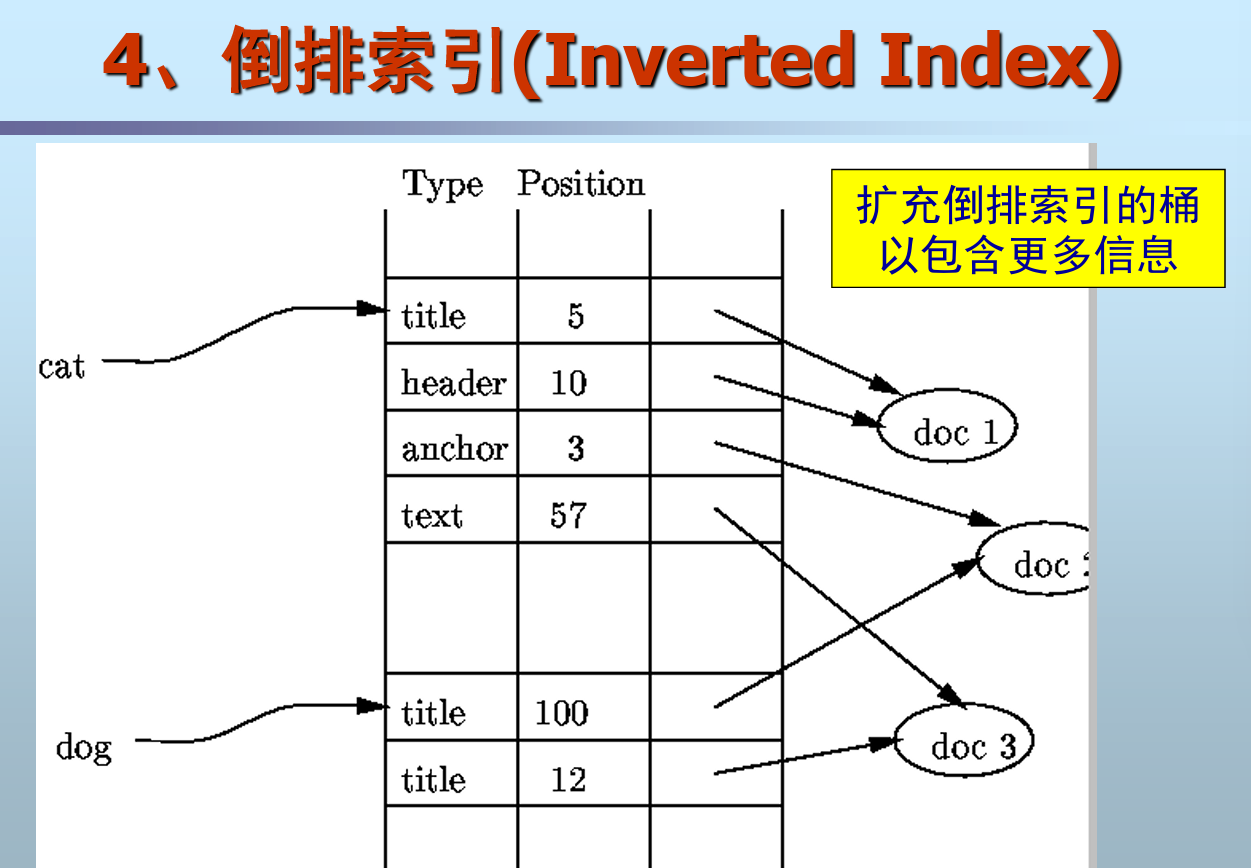
倒排索引

• 应用于文档检索，与辅助索引思想类似
• 不同之处
  • 记录→文档
  • 记录查找→文档检索
  • 查找键→文档中的词
• 思想
  • 为每个检索词建立间接桶
  • 桶的指针指向检索词所出现的文档

B+树

• 一种树型的多级索引结构
• 树的层数与数据大小相关，通常为3层
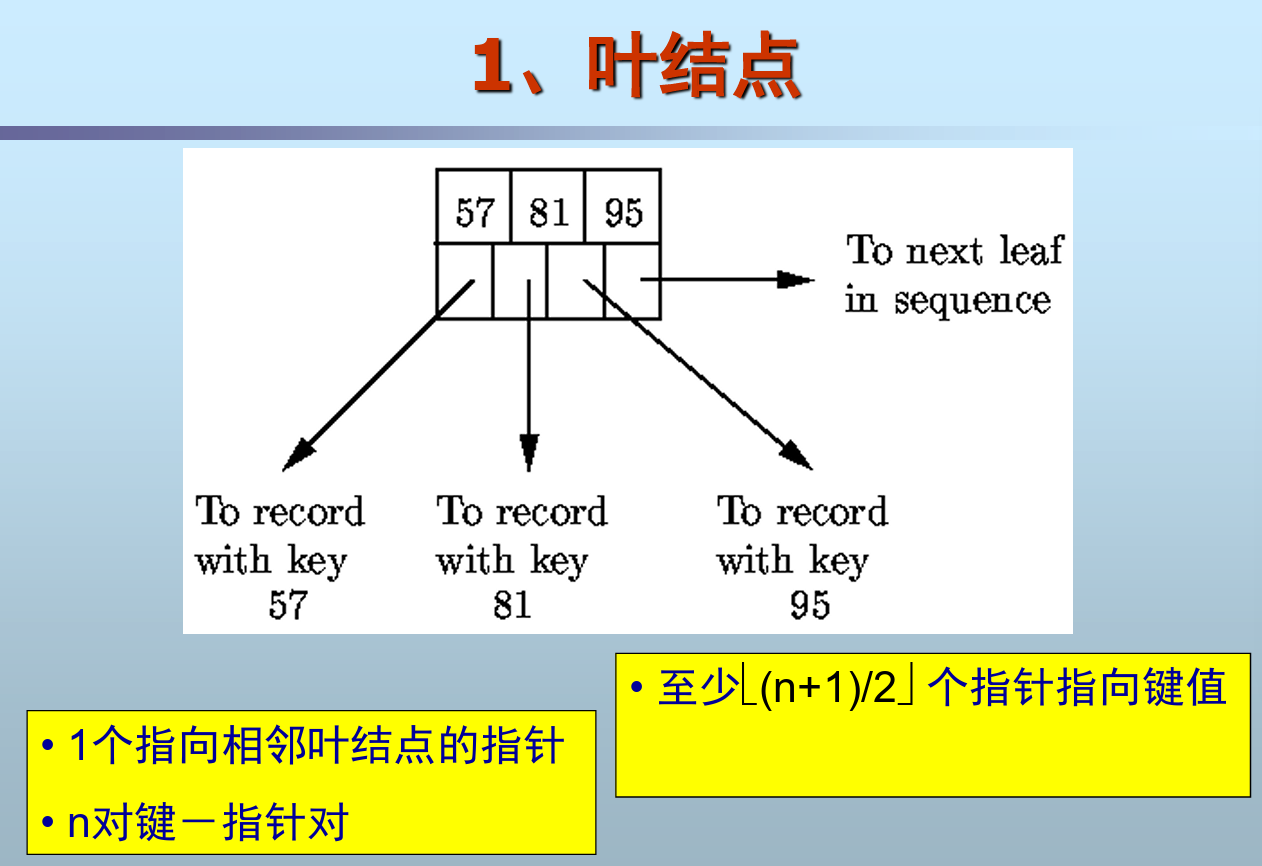
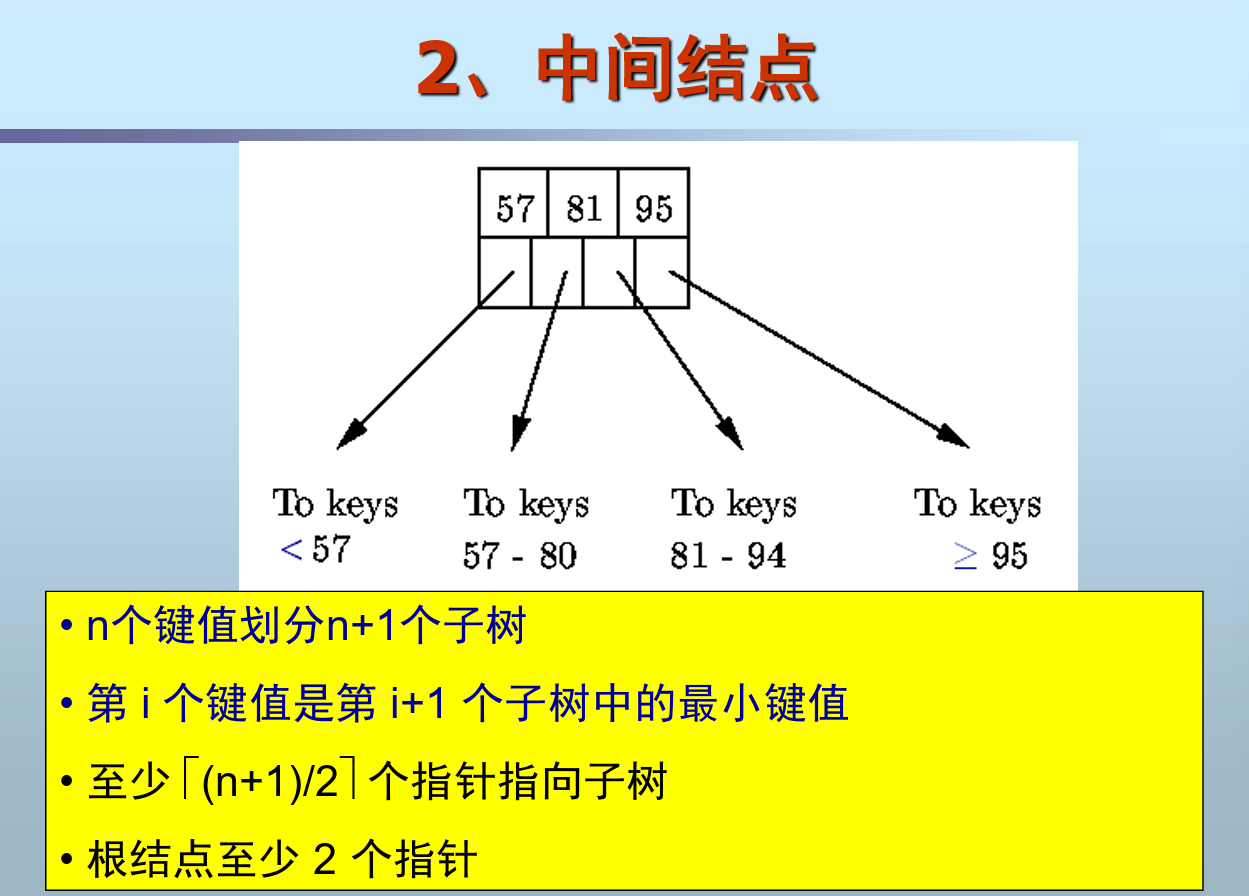
• 所有结点格式相同：n个值，n＋1个指针
• 所有叶结点位于同一层

叶结点

非叶结点

若树中结点最多含有n个关键字，则每个分支结点至少有 ⌈(n+1)/2⌉ 棵子树（n+1 即B+树的阶）

区间划分左闭右开

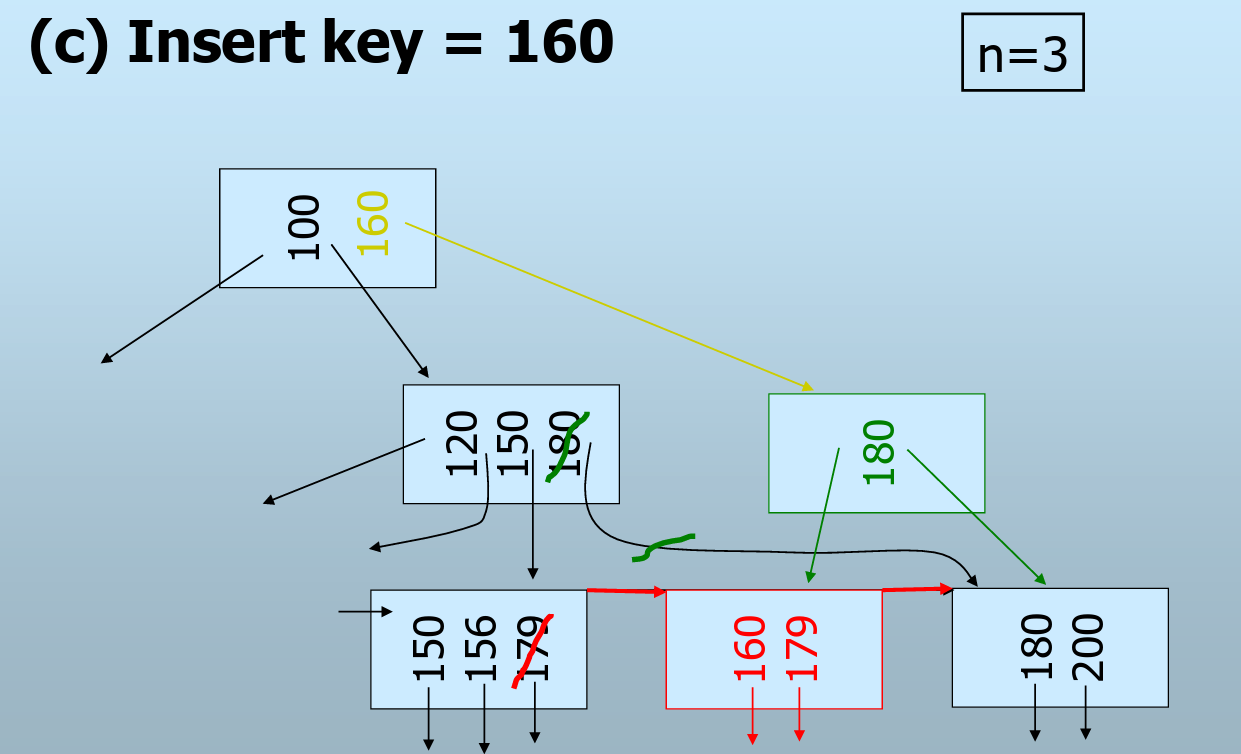
插入

• 查找插入叶结点
• 若叶结点中有空闲位置（键），则插入
• 若没有空间，则分裂叶结点
  • 叶结点的分裂可视作是父结点中插入一个子结点
  • 递归向上分裂，非叶结点的分裂会将本层的一个键值移动到上一层
  • 分裂过程中需要对父结点中的键加以调整
  • 例外：若根结点分裂，则需要创建一个新的根结 点

删除

查找要删除的键值，并删除之。

若结点的键值填充低于最低规定值，则调整：

• 隔壁有多的元素：若相邻的叶结点中键填充高于最低规定值，则将其中 一个键值移到该结点中
• 隔壁没有多的元素：合并该结点与相邻结点
  • 合并可视作在父结点中删除一个子结点
• 递归向上删除 若删除的是叶结点中的最小键值，则需对父 结点的键值加以调整

B+树的效率

• 访问索引的I/O代价＝树高（B＋树不常驻内 存）或者0（常驻内存）
• 树高通常不超过3层，因此索引I/O代价不超 过3（总代价不超过4读取记录）
• 通常情况下，根节点常驻内存，因此索引I/O代 价不超过2（总代价不超过3）

散列索引

• 对于给定的散列键值k，计算h(K)
• 根据h(K)定位桶
• 查找桶中的块

插入删除：考虑溢出块

空间利用率 = 实际键值数 / 所有桶可放置的键值数

动态散列表

可扩展散列表（Extensible Hash Tables）

机制

• 散列函数值h(k)是一个b(足够大)位二进制序列 ，前 i 位表示桶的桶号。
• i 的值随数据文件的增长而增大，导致成倍增加桶数目

优点

• 当查找记录时，只需查找一个存储块。

缺点

• 桶增长速度快，可能会导致内存放不下整个 桶数组，影响其他保存在主存中的数据，波 动较大。

线性散列表（Linear Hash Tables）

机制

• h(k)仍是二进制位序列，但使用右边（低）i 位 区分桶
• 桶数＝n，h(k)的右 i 位＝m
• 若m < n，则记录位于第m个桶
• 若n ≤ m < 2i，则记录位于第 m- 2^(i - 1) 个桶
• n的选择：总是使n与当前记录总数r保持某个固定 比例
• 意味着只有当桶的填充度达到超过某个比例后桶数才开 始增长

看作业习题