查询执行
复习提纲
1、嵌套循环连接
2、归并连接
3、索引连接
4、散列连接
5、连接算法的I/O代价估计与内存开销*
物理查询计划操作符
- 逻辑操作符的物理操作符
- 逻辑操作符的特定实现
- 其它物理操作符
- 表扫描:TableScan
- 排序扫描:SortScan
- 索引扫描:IndexScan

连接操作的实现算法(*)
嵌套循环连接
暴力遍历算法
归并连接
- 若无序先排序,这里按升序排序
- 在暴力遍历的基础上,通过排序使得R2的指针不回退
- 因为可能有重复值,输出元组的算法要特别别注意


索引连接
对于R1的每个值,用索引来找到R2中对应属性与它相等的元组集,拼接即可输出
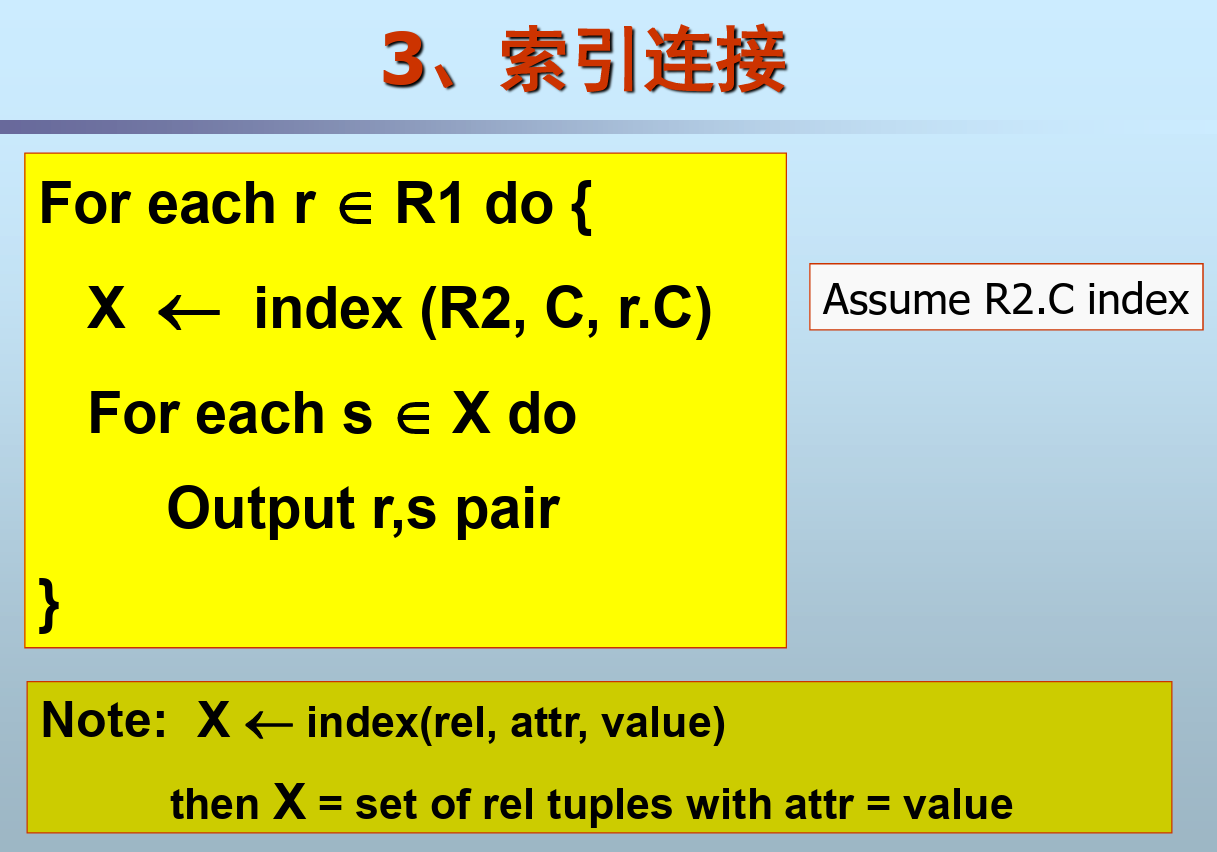
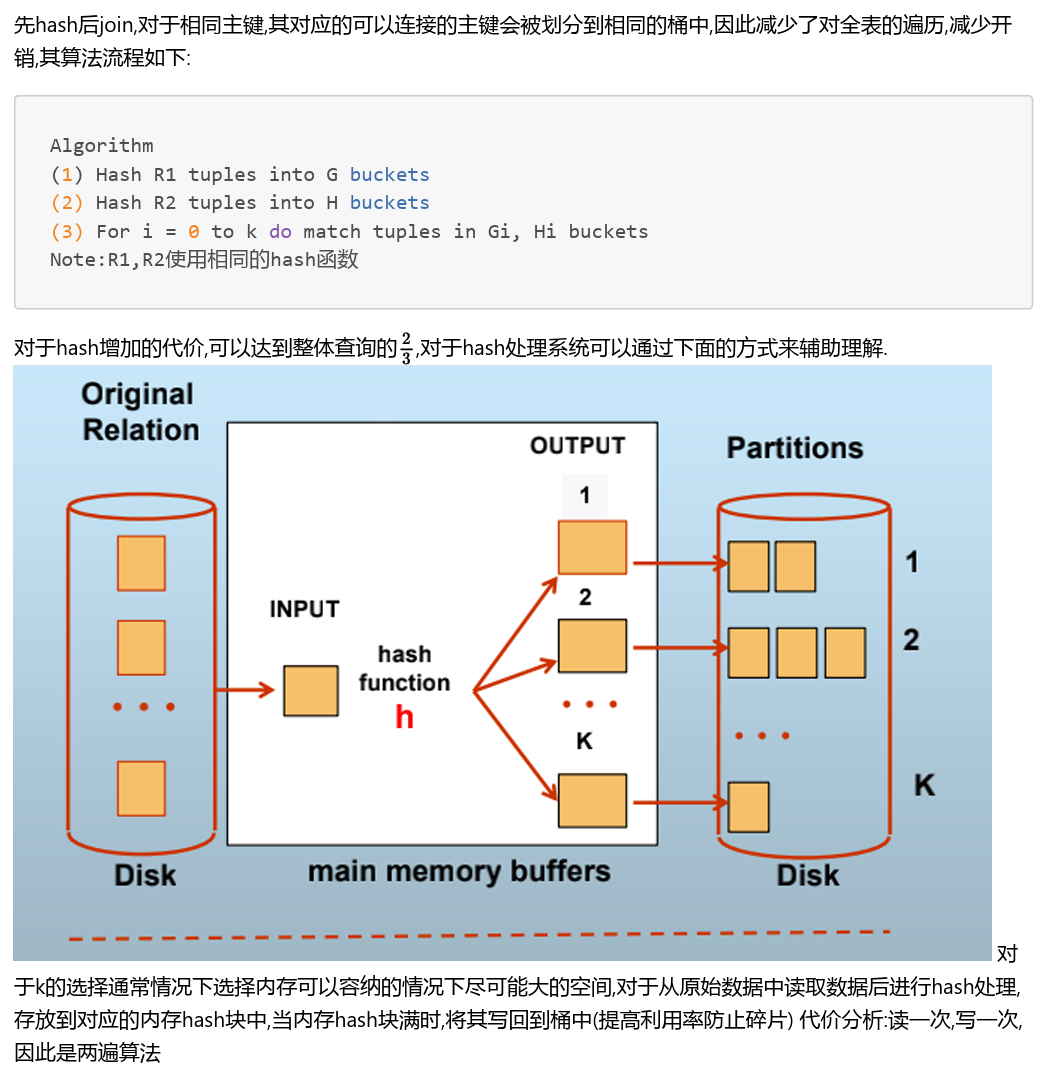
散列连接
使用同样的哈希函数,且若能保证不同键值的桶一定不相同,那么下标相同的桶中的键值是一样的,可以通过全组合拼接出输出元组;若不同键值放在同一个桶中,仍然需要遍历匹配。
连接算法的I/O代价估计
影响连接算法代价(I/O)的因素
- 关系的元组是否在磁盘块中连续存放? (contiguous?)
- 关系是否按连接属性有序? (ordered?)
- 连接属性上是否存在索引? (indexed?)
嵌套循环连接代价
元组不连续存放
元组可能分散在完全不同的块里,元组数 = 块数
暴力遍历
- 每个元组都放在不同的块里,所以每次访问一个元组都要读一次
- IO代价 = R1元组数 * ( 1 + R2元组数 )
改进的策略
- 暴力算法中R2的每个元组都被读入内存中 T(R1) 次进行匹配
- 空间换时间,将R1元组尽可能读入内存中,R2元组每次进入内存可以与1000条R1的元组匹配,只需读入10次
- 进一步改善:交换R1,R2的连接顺序,让少的在左边
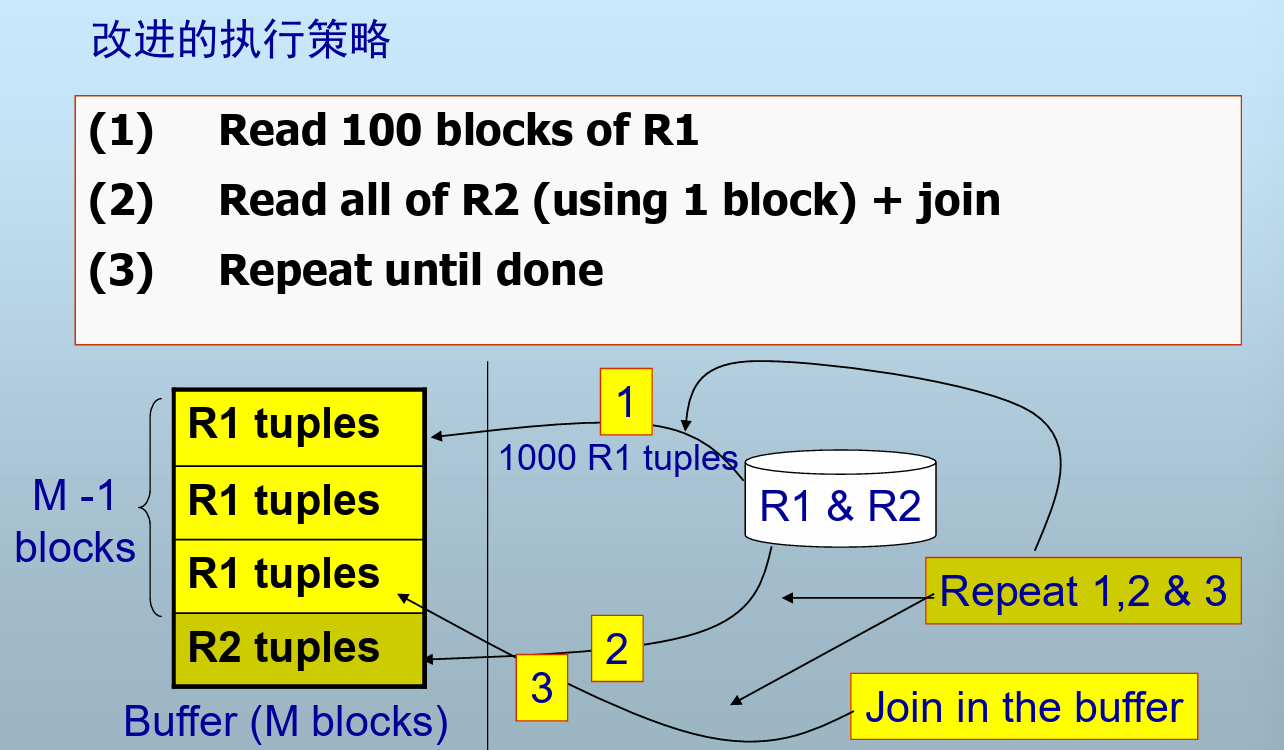
元组连续存放
用上述的改进算法思想,每一轮读100个R2的块进内存和每个R1的记录进行匹配

归并连接代价
连续存放
已排序的情形
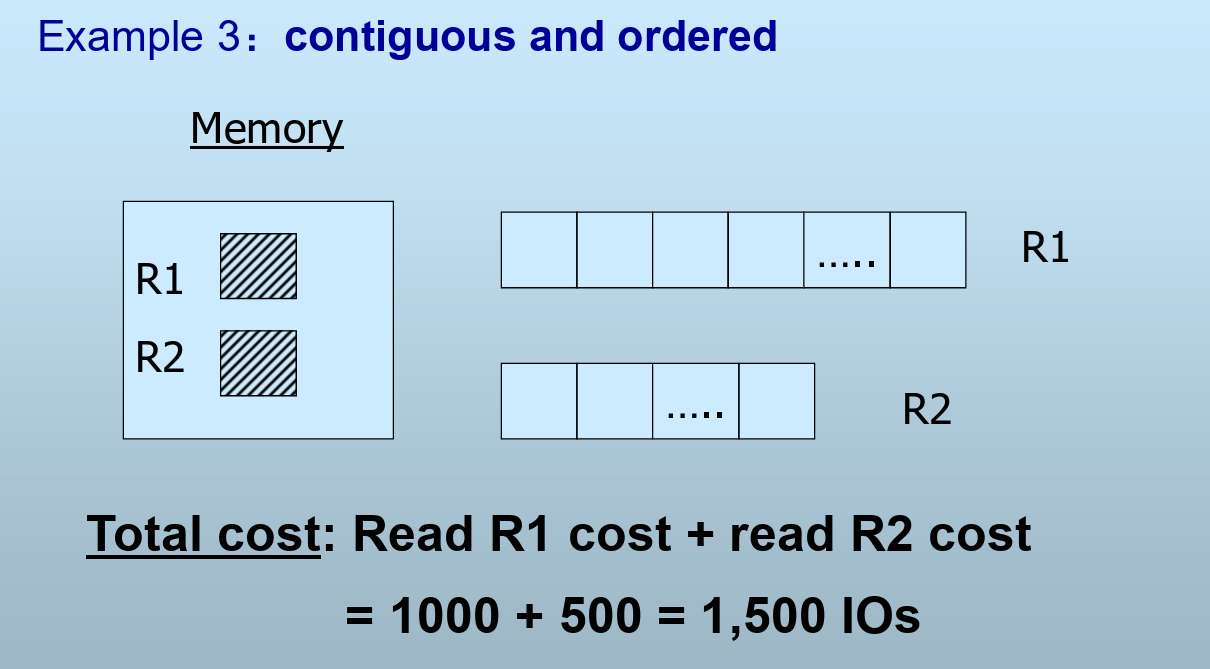
未排序则先排序
排序方法:两阶段多路归并
- 第一阶段:尽可能多的块读入内存中并排序成chunk,写回磁盘(图中一个chunk是100个块那么大)
- 按外部归并排序将多个chunk归并,缓存中每次比较产生一个最小元组写回磁盘

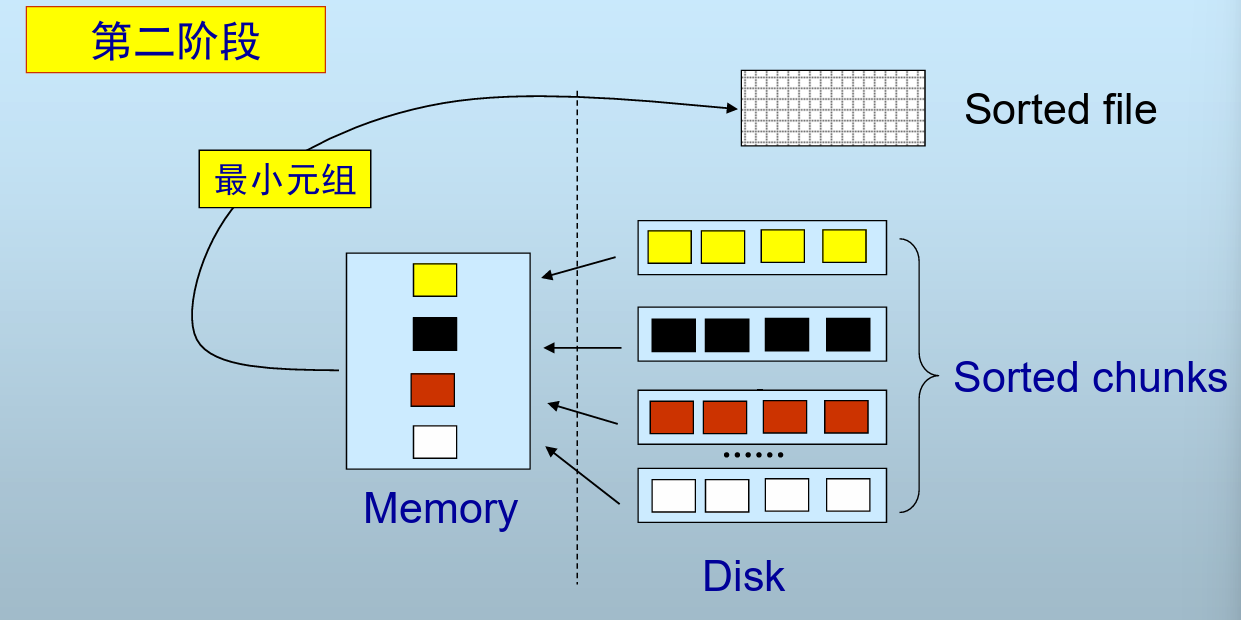
代价分析
- 排序代价:每个元组均被读入两次,写回两次,四次I/O
- 归并和连接代价:每个元组读入一次,一次I/O
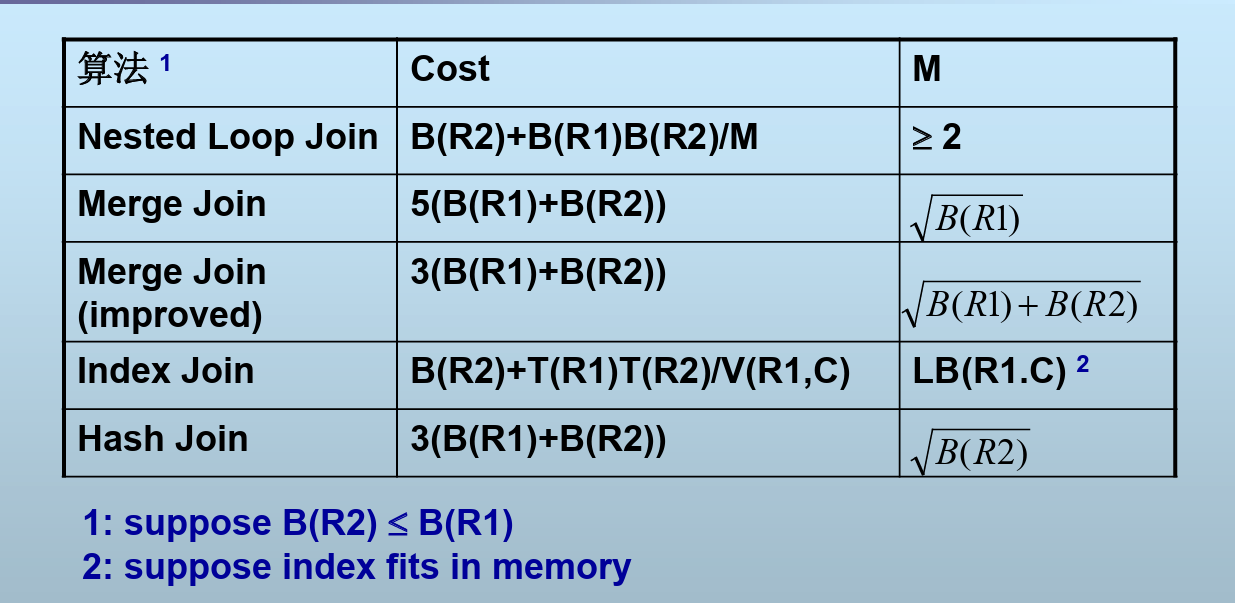
归并连接和嵌套循环连接的比较

内存需求

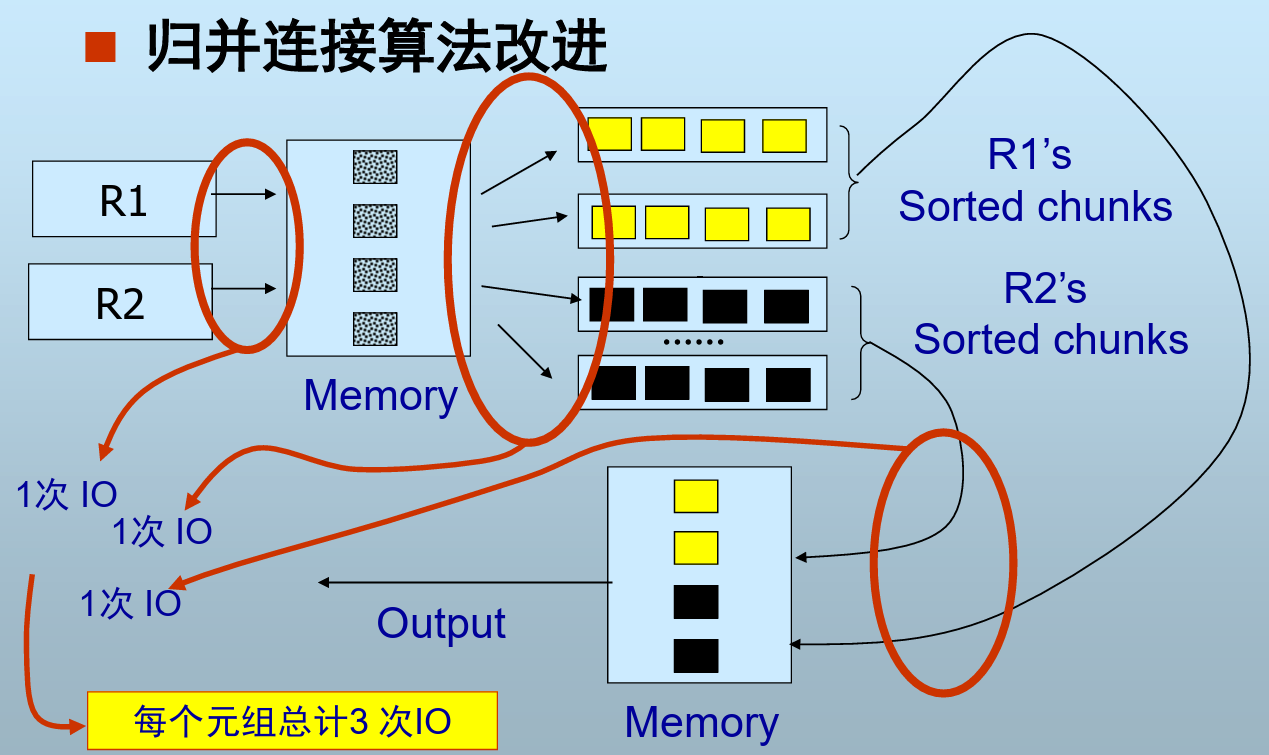
归并连接算法的改进
- 使用条件:R1 chunks + R2 chunks <= M
- 第一阶段将记录排序为chunk不变
- 第二阶段排序和join一起进行
- 每次需要将R1和R2的各一个块读入

这样每个元组只需3次I/O
chunk还没归并怎么实现join的??—— R1 chunks + R2 chunks <= M
索引连接代价
假设
- R1.C 建立了索引
- R1.C 的索引在内存中
- R2 记录连续存放,未排序

代价分析
- 读入R2的每个元组 = 500次I/O
- 查内存中R1的索引 = 0次I/O
- 若有匹配的记录则读入内存中join,I/O次数考虑选中率
- 若R1.C是主键, R2.C是外键,则 每个R2 tuple在R1中,选中率 p =1
- 若V(R1,C)=5,000, T(R1) = 10,000, 则 每个R2 tuple在R1中的选中率 p = T(R1)/V(R1,C)=2
若R1的索引不能全部读入内存中
- 读入:所有的2级索引块 + 尽量多的1级索引块
- 若对应记录的1级索引块在内存中,则I/O次数 = 0,否则多一次I/O

散列连接代价
连续存放且未排序,100个桶
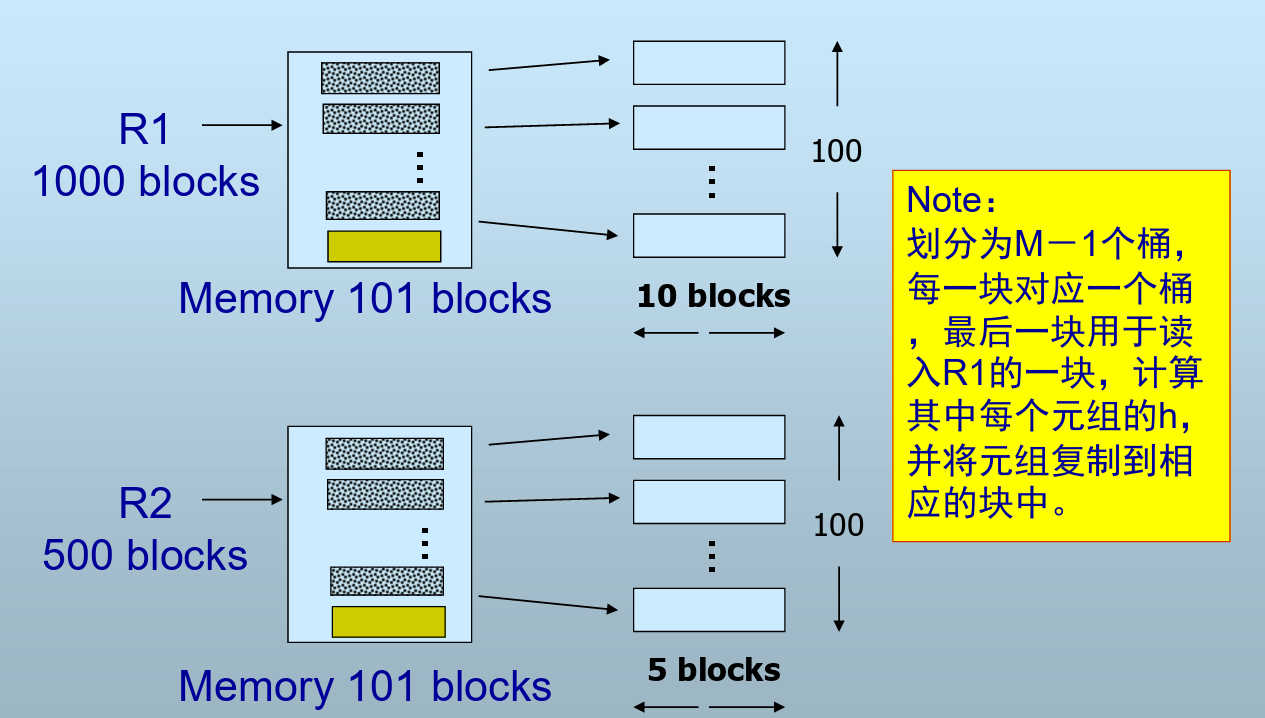
代价分析
总共3次I/O
- R1读入,创建桶,写回
- R2读入,创建桶,写回
- 读入R2一个桶,读入R1对应的桶并join
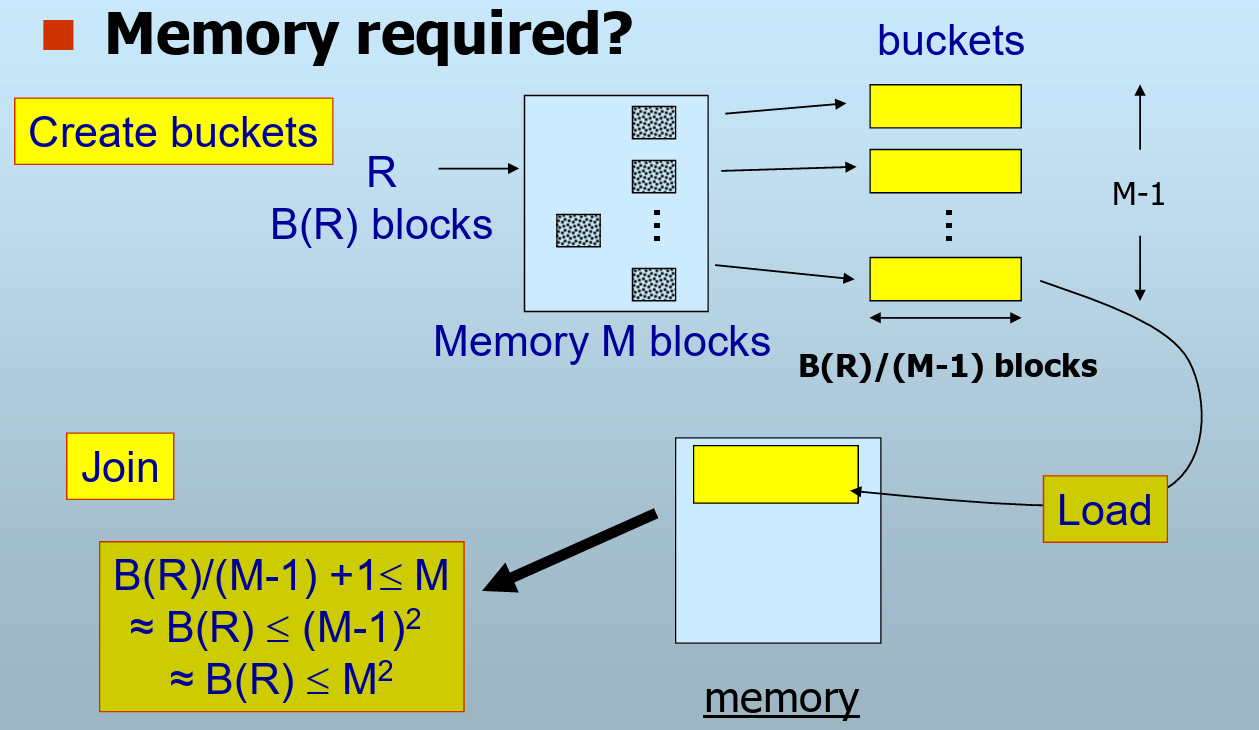
内存需求
JOIN的需求:一个桶中的块数 + 1 <= 内存块数
近似:Min( B(R1), B(R2) ) <= M^2